
Data Science para marketing
Creado por Nicolás Labbé
Fine tuning de algoritmos de clasificación
Introducción
Supongamos que usted es el responsable de aprendizaje automático en una empresa de análisis de marketing. Su empresa ha asumido un proyecto de Amazon para predecir si un usuario comprará un producto durante las campañas de rebajas de la temporada navideña.
Se le han proporcionado datos anónimos sobre la actividad de los clientes en el sitio web de Amazon: número de productos comprados, precios, categorías, etc.
En estos escenarios, donde la variable objetivo es un valor discreto (por ejemplo, si el cliente comprará el producto o no), los problemas se denominan problemas de clasificación.
Actualmente, existe una gran cantidad de algoritmos de clasificación disponibles para resolver estos problemas, y elegir el adecuado es crucial. Por lo tanto, primero explorará el conjunto de datos para obtener algunas observaciones al respecto.
A continuación, probarás diferentes algoritmos de clasificación y evaluará las métricas de rendimiento de cada modelo para determinar si es lo suficientemente bueno como para que la empresa lo utilice.
Finalmente, obtendrá el mejor algoritmo de clasificación de todos los modelos entrenados, que se utilizará para predecir si un usuario comprará un producto durante la oferta.
En este capítulo, trabajarás en problemas como estos para comprender cómo elegir el algoritmo de clasificación adecuado evaluando su rendimiento con diversas métricas.
Seleccionar las métricas de rendimiento adecuadas, optimizar, ajustar y evaluar el modelo es fundamental para construir cualquier modelo de aprendizaje automático supervisado. Además, elegir un modelo de aprendizaje automático adecuado es un arte que requiere experiencia, y cada algoritmo tiene sus ventajas y desventajas.
Support Vector Machine (SVM)
- Algoritmo de aprendizaje supervisado usado para clasificación y regresión.
- Encuentra el hiperplano óptimo que separa clases de manera clara.
- Se enfoca en los puntos de datos más cercanos al hiperplano: vectores de soporte.
¿Cómo funciona SVM?
- Identifica un hiperplano que maximiza el margen entre clases.
- El margen es la distancia entre el hiperplano y los vectores de soporte más cercanos.
- El mejor modelo tiene el margen más amplio posible.
 Figura 12.01 - Un conjunto de modelos de árboles
Figura 12.01 - Un conjunto de modelos de árboles
Ventajas de SVM
- Funciona bien con espacios de alta dimensión.
- Robusto frente al overfitting en problemas de clasificación binaria.
- Puede ser eficiente con datasets pequeños y medianos.
Desventajas de SVM
- No escala bien con datasets muy grandes.
- La elección del kernel y sus parámetros puede ser compleja.
- Difícil de interpretar comparado con modelos lineales.
Aplicaciones comunes
- Clasificación de texto (spam vs no spam).
- Reconocimiento facial.
- Detección de fraudes.
- Diagnóstico médico.
Datos Linealmente Separables
- Dos clases pueden separarse con una línea recta (en 2D) o un hiperplano (en dimensiones superiores).
- En este caso, SVM busca el hiperplano que maximiza el margen entre ambas clases.
- Los vectores de soporte son los puntos más cercanos al hiperplano y definen su posición.
Ideal para aplicar un SVM lineal sin necesidad de transformar el espacio.
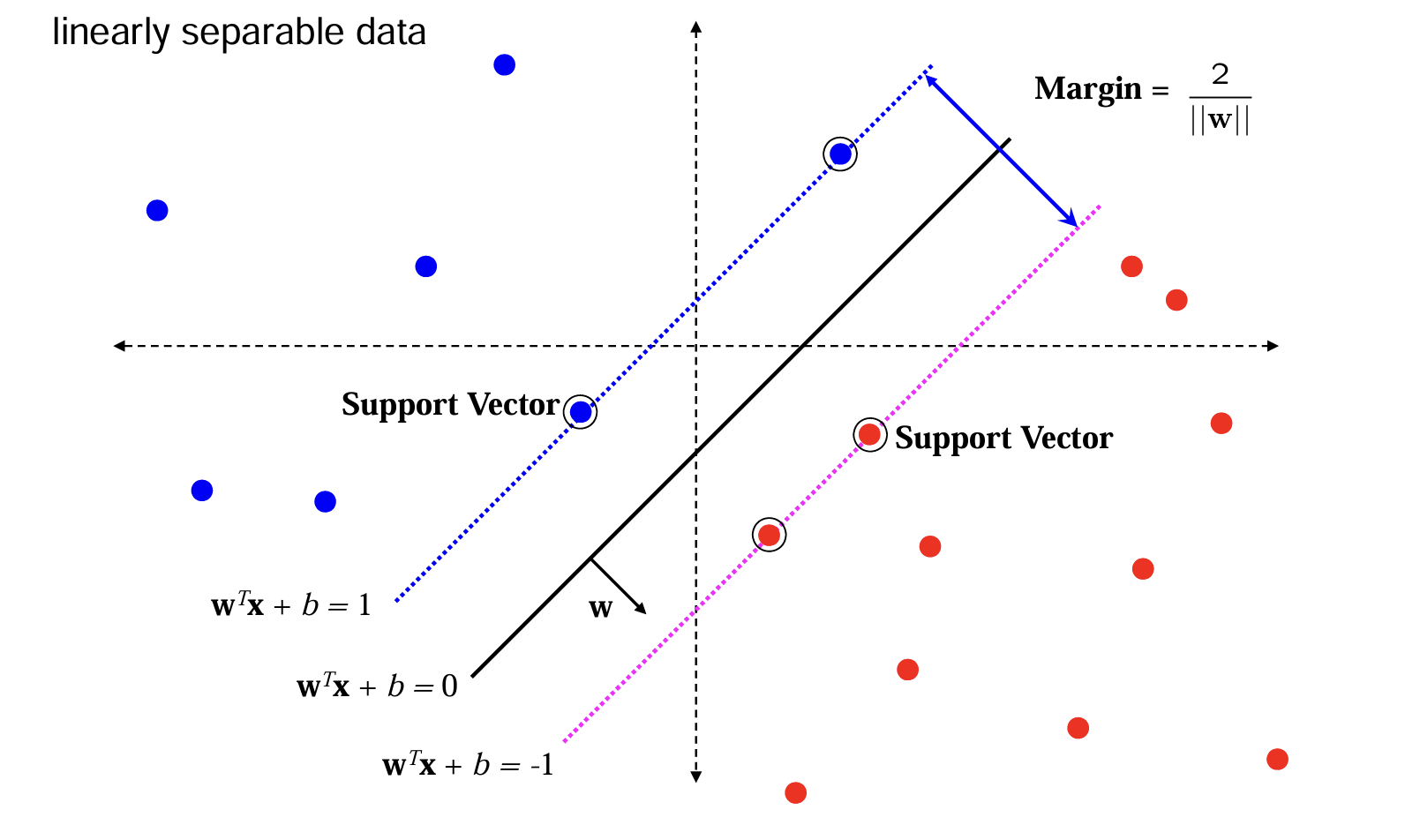 Figura 12.03 - Linealmente separables
Figura 12.03 - Linealmente separables
¿Qué pasa si los datos no son linealmente separables?
- Se puede aplicar el truco del kernel.
- Transforma los datos a un espacio de mayor dimensión donde sí sean separables.
- Ejemplos de kernels: lineal, polinómico, radial (RBF), sigmoide.
 Figura 12.03 - Linealmente no separables
Figura 12.03 - Linealmente no separables
 Figura 12.03 - Linealmente no separables
Figura 12.03 - Linealmente no separables
¿Qué es el truco del kernel?
- Es una técnica que permite aplicar SVM en datos no linealmente separables.
- Transforma los datos a un espacio de mayor dimensión donde sí puedan separarse linealmente.
- Evita calcular explícitamente la transformación, usando funciones de similitud llamadas kernels.
¿Por qué es útil el truco del kernel?
- Muchos problemas del mundo real no son linealmente separables en su espacio original.
- El truco del kernel permite encontrar límites de decisión no lineales.
- Es computacionalmente eficiente porque calcula productos escalares en el espacio transformado sin necesidad de hacerlo explícitamente.
Ejemplo conceptual
- Imagina un conjunto de datos en forma de anillos concéntricos (círculos).
- En 2D, son inseparables linealmente.
- Al aplicar una transformación a 3D, se vuelven separables por un plano.
- El kernel permite hacer esto sin transformar realmente los datos.
Tipos comunes de kernel
- Lineal: sin transformación (caso base).
- Polinómico: permite bordes de decisión curvos.
- Radial Basis Function (RBF): separa con regiones circulares o elípticas.
- Sigmoide: similar a una red neuronal.
Resumen: truco del kernel
- Permite aplicar SVM a problemas no lineales sin transformaciones costosas.
- Utiliza funciones matemáticas que operan en el espacio original pero imitan transformaciones complejas.
- Clave para extender el poder de SVM a problemas complejos de clasificación.
Ejercicio 12.01: Entrenamiento de un algoritmo SVM con un conjunto de datos
En este ejercicio, trabajará con el conjunto de datos Shill Bidding, cuyo archivo se llama Shill_Bidding_Dataset.csv. Puede descargar este conjunto de datos desde el siguiente enlace: https://packt.link/GRn3G. Este es el mismo conjunto de datos que conoció en el Ejercicio 7.01, Comparación de predicciones mediante regresión lineal y logística con el conjunto de datos Shill Bidding. Su objetivo es utilizar esta información para predecir si una subasta muestra un comportamiento normal o no (0 significa comportamiento normal y 1 significa comportamiento anormal). Utilizará el algoritmo SVM para construir su modelo:¿Qué es un árbol de decisión?
- Algoritmo de aprendizaje supervisado usado principalmente para clasificación.
- No paramétrico: no requiere definir parámetros como kernel, C o gamma.
- Usa una estructura en forma de árbol para tomar decisiones.
- Cada nodo representa una regla basada en alguna variable.
¿Cómo funciona?
- En cada nodo, se evalúa una condición del tipo: ¿Variable X > valor?
- La respuesta (sí/no) define una rama del árbol.
- Este proceso continúa hasta llegar a una predicción (hoja).
- Se pueden usar para clasificación o regresión con pequeños ajustes.
Ventajas de los árboles de decisión
- Fáciles de entender y visualizar.
- Manejan tanto datos numéricos como categóricos.
- Requieren poca limpieza de datos (toleran datos faltantes).
- No hacen suposiciones sobre la distribución de los datos.
- Modelo explicativo (white-box): las reglas pueden interpretarse fácilmente.
Desventajas de los árboles de decisión
- Tendencia al overfitting; es necesario aplicar pruning.
- No funcionan bien con datos desbalanceados.
- En casos desbalanceados, favorecen la clase mayoritaria y pierden capacidad de generalización.
- Requieren técnicas adicionales (como balanceo de clases) para buenos resultados.
Resumen
- Los árboles de decisión son potentes, interpretables y versátiles.
- Ideales para problemas donde se requiere explicabilidad.
- Se deben usar con cuidado para evitar sobreajuste y sesgos por desbalance.
¿Y los parámetros como kernel, C y gamma?
- En SVM, es necesario definir varios hiperparámetros:
- Kernel: función para transformar el espacio (lineal, RBF, etc.).
- C: penalización por errores de clasificación (trade-off entre margen y errores).
- Gamma: define la influencia de cada punto (usado en kernels como RBF).
- En árboles de decisión, no necesitas especificar estos parámetros.
- Esto los hace más simples de configurar y entender, aunque pueden requerir poda o ajuste de profundidad para evitar sobreajuste.
Ejercicio 12.02: Implementación de un algoritmo de árbol de decisión sobre un conjunto de datos
En este ejercicio, utilizará árboles de decisión para construir un modelo sobre el mismo conjunto de datos de subastas que utilizó en el ejercicio anterior. Esta práctica de entrenar diferentes clasificadores en el mismo conjunto de datos es muy común en cualquier tarea de clasificación. Entrenar múltiples clasificadores de diferentes tipos facilita la selección del clasificador adecuado para una tarea.
Estructura de un árbol de decisión
- Árbol invertido: la raíz está en la parte superior, las hojas en la parte inferior.
- Nodo: bloque que contiene una regla de decisión.
- Raíz: el nodo inicial, donde comienza la evaluación.
- Hojas: nodos terminales que entregan la predicción.
- El flujo va de la raíz a una hoja según las reglas de decisión.
Terminología clave
- Nodo: punto de decisión basado en una variable.
- Rama: resultado de una condición (sí/no, mayor/menor, etc.).
- Hoja: resultado final del árbol (clase o valor predicho).
- Árbol completo: conjunto de nodos y ramas que forman un modelo de decisión.
¿Cómo se elige qué variable usar en un nodo?
- Se evalúan todas las variables disponibles.
- Se selecciona la que produce los subconjuntos más “puros”.
- La pureza se mide con funciones como:
- Ganancia de información
- Impureza de Gini
- Entropía
- Error de clasificación
Ganancia de información
- Cuantifica la reducción de incertidumbre después de una división.
- Cuanto mayor sea la ganancia de información, mejor es la división.
- Basada en la medida de entropía.
Entropía
- Mide la cantidad de desorden o impureza en los datos.
- Entropía baja = grupo homogéneo.
- Entropía alta = mezcla de clases.
Impureza de Gini
- Mide la probabilidad de clasificar incorrectamente un dato al azar.
- Menor valor = mayor pureza.
- Muy utilizada por su eficiencia computacional.
Error de clasificación
- Proporción de observaciones mal clasificadas en un nodo.
- Menos sensible que Gini o entropía, por eso se usa menos.
- Útil en algunas tareas exploratorias o como métrica secundaria.
Resumen
- Los árboles se construyen dividiendo los datos en base a variables que maximizan la pureza.
- Los criterios como Gini, entropía y ganancia de información guían esta elección.
- El árbol final es un modelo de flujo desde raíz a hojas, donde se realiza la predicción.
¿Qué es Random Forest?
- Es un algoritmo de ensamble basado en árboles de decisión.
- Reduce el overfitting promediando los resultados de múltiples árboles.
- Cada árbol individual puede sobreajustar, pero el conjunto mejora la generalización.
Problema con árboles individuales
- Los árboles de decisión tienden a aprender ruido o patrones aleatorios si no se podan.
- Ejemplo: recomendar productos por coincidencias accidentales (como recomendar beard wash a mujeres).
- Esto daña la capacidad del modelo para predecir correctamente en nuevos casos.
¿Cómo soluciona esto Random Forest?
- Entrena múltiples árboles de decisión con diferentes subconjuntos de datos y características.
- Luego combina (promedia o vota) los resultados para obtener una predicción más robusta.
- Esto reduce la varianza del modelo y mejora su generalización.
Random Forest como método de ensamble
- Random Forest pertenece a una familia de métodos llamada ensemble learning.
- Combina múltiples clasificadores para mejorar precisión y estabilidad.
- Los dos tipos principales de ensamble son:
- Bagging (Bootstrap Aggregating)
- Boosting
Bagging
- Los datos se dividen aleatoriamente en subconjuntos.
- Se entrena un modelo (por ejemplo, árbol) sobre cada subconjunto de forma independiente.
- Las predicciones se combinan (promedio o mayoría).
- Random Forest es un ejemplo de bagging.
- Principal objetivo: reducir la varianza.
Boosting
- Los modelos se construyen secuencialmente.
- Cada nuevo modelo intenta corregir los errores del anterior.
- Se combinan modelos débiles para formar uno fuerte.
- Ejemplos: XGBoost, LightGBM, CatBoost.
- Principal objetivo: reducir el sesgo.
Resumen
- Random Forest: combina árboles para mejorar precisión y evitar sobreajuste.
- Es un método de bagging que mejora la estabilidad del modelo.
- Parte de una familia más amplia de técnicas de ensamble que también incluye boosting.
¿Cómo funciona Random Forest?
El proceso completo se basa en generar múltiples árboles y combinarlos. Veamos los pasos uno a uno:
Paso 1: Bootstrap Sampling
- Se crean muestras aleatorias con reemplazo desde el conjunto de entrenamiento.
- Ejemplo:
Data1, Data2, ..., Datak. - Esto asegura que cada árbol vea un subconjunto diferente del total.
Paso 2: Entrenamiento de árboles
- Se entrena un árbol de decisión en cada muestra bootstrap.
- Los árboles se denominan
Learner1, Learner2, ..., Learnerk. - Estos árboles son independientes entre sí.
Paso 3: Selección aleatoria de características
- En cada nodo, se eligen aleatoriamente d características sin reemplazo.
- Esto introduce diversidad adicional entre los árboles.
Paso 4: División de nodos
- Cada nodo se divide utilizando solo las d características seleccionadas.
- El criterio de división puede ser ganancia de información, Gini, etc.
- Esto evita que todos los árboles tomen decisiones idénticas.
Paso 5: Repetición del proceso
- Los pasos 1 a 4 se repiten k veces (por ejemplo, 100 árboles).
- Esto genera
Model1, Model2, ..., Modelk.
Paso 6: Agregación de resultados
- Se toman todas las predicciones de los árboles.
- Se combinan mediante votación por mayoría (en clasificación) o promedio (en regresión).
- Este paso es el Model Combiner.
Resumen del proceso
- Crear muestras bootstrap del entrenamiento.
- Entrenar árboles independientes con diferentes muestras.
- Usar subconjuntos aleatorios de características en cada división.
- Combinar las predicciones para mayor robustez.
Ventajas de Random Forest
- Reduce el overfitting al promediar múltiples predicciones.
- Permite calcular la importancia de las variables.
- Se puede usar tanto para clasificación como para regresión.
- Maneja bien datasets desbalanceados.
- Es robusto frente a datos faltantes.
Desventajas de Random Forest
- Puede tener sesgo (aunque reduce la varianza).
- Es un modelo tipo black-box: difícil de interpretar o explicar.
Resumen
- Random Forest es un algoritmo poderoso y flexible.
- Ideal cuando se necesita robustez y no se requiere alta interpretabilidad.
- Muy útil para tareas reales con datos ruidosos o incompletos.
Ejercicio 8.03: Implementación de un modelo de bosque aleatorio sobre un conjunto de datos
En este ejercicio, utilizará un bosque aleatorio para construir un modelo sobre el mismo conjunto de datos de subasta utilizado anteriormente. Asegúrese de utilizar el mismo cuaderno de Jupyter que el utilizado en el ejercicio anterior:
Algoritmos clásicos: comparación de la precisión
En las secciones anteriores, analizamos las matemáticas de cada algoritmo y aprendimos sobre sus ventajas y desventajas. Mediante tres ejercicios, implementó cada algoritmo en el mismo conjunto de datos. En la Figura 8.32, puede ver un resumen de los porcentajes de precisión obtenidos. Volviendo al caso práctico de Amazon que analizamos al principio del capítulo, es evidente que elegiría el clasificador de árbol de decisión para predecir si un cliente comprará un producto durante las rebajas:
Comparación de Precisión entre Clasificadores
| Classifier | Accuracy Percentage |
|---|---|
| SVM | 97.75% |
| Decision Tree | 99.81% |
| Random Forest | 98.96% |
Preprocesamiento de datos para modelos de aprendizaje automático
¿Por qué transformar variables numéricas?
Muchos algoritmos de Machine Learning se ven afectados por la escala o distribución de las variables.
- Variables con distintas magnitudes pueden sesgar modelos.
- Modelos basados en distancia o gradiente requieren datos comparables.
- Las técnicas de transformación ayudan a mejorar el rendimiento del modelo.
Scaling (Escalado)
Transforma las variables para que estén dentro de un mismo rango, típicamente entre 0 y 1.
- Fórmula: (X - min) / (max - min)
- Usos: KNN, clustering, redes neuronales
- Problema: Sensible a valores extremos (outliers)
Standardization (Estandarización)
Centra los datos en media 0 y los escala por su desviación estándar.
- Fórmula: (X - μ) / σ
- Usos: Regresión lineal, SVM, PCA
- Ventaja: Preserva la forma de la distribución
Normalization (Normalización)
Escala cada fila (registro) para que tenga norma igual a 1 (L2).
- Fórmula: X / ‖X‖
- Usos: Modelos con vectores como NLP o deep learning
- Nota: No se aplica por columna, sino por fila
Comparación de técnicas (Parte 1)
| Característica | Standardization | Scaling (Min-Max) | Normalization (L2) |
|---|---|---|---|
| Nombre en español | Estandarización | Escalado | Normalización |
| Fórmula | (X - μ) / σ | (X - min) / (max - min) | X / ‖X‖ |
| Media resultante | 0 | Variable | No aplica |
| Desviación estándar | 1 | Variable | No aplica |
| Preserva distribución | Sí | No | No |
Comparación de técnicas (Parte 2)
| Característica | Standardization | Scaling (Min-Max) | Normalization (L2) |
|---|---|---|---|
| Transformación | Por columna | Por columna | Por fila |
| Rango final | Abierto | [0, 1] | Norma = 1 |
| Uso típico | Regresión, SVM, PCA | KNN, Clustering, Deep Learning | NLP, vectores de texto |
| Sensibilidad a outliers | Media | Alta | Alta |