Data Science para marketing
Creado por Nicolás Labbé
Aprendizaje supervisado
Introducción
El éxito de una empresa depende en gran medida de su capacidad para atraer nuevos clientes y fidelizar a los existentes. La pérdida de clientes se refiere a la situación en la que un cliente deja de usar su producto y abandona la empresa. La pérdida de clientes puede ser cualquier cosa: la pérdida de un empleado de una empresa, la pérdida de un cliente de una suscripción móvil, etc.
Predecir la pérdida de clientes es importante para una organización porque captar nuevos clientes es fácil, pero retenerlos es más difícil. De igual manera, una alta tasa de pérdida de empleados también puede afectar a una empresa, ya que estas invierten grandes cantidades de dinero en la formación de talento.
Asimismo, las organizaciones con altas tasas de retención se benefician de un crecimiento constante, lo que también puede generar un alto número de recomendaciones de clientes existentes. La predicción de la pérdida de clientes es uno de los casos de uso más comunes del aprendizaje automático.
Aprendió sobre el aprendizaje supervisado en los capítulos anteriores, donde adquirió experiencia práctica en la resolución de problemas de regresión. En cuanto a la predicción de la pérdida de clientes, encontrará que la mayoría de los casos de uso implican tareas de clasificación supervisadas. Por eso, comenzará este capítulo aprendiendo sobre los problemas de clasificación.
A continuación, aprenderá sobre el algoritmo de regresión logística. No solo comprenderá la intuición detrás de este algoritmo, sino también su implementación. A continuación, verá cómo organizar los datos para construir un modelo de abandono, seguido de una exploración de los datos para ver si se pueden extraer inferencias estadísticas.
Descubrirá cuáles son las características importantes para construir su modelo de abandono y, finalmente, aplicará la regresión logística para predecir el abandono de clientes. A lo largo del capítulo, trabajará con un caso práctico de predicción del abandono de clientes para comprender e implementar los conceptos anteriores.
Al final del capítulo, habrá construido un modelo que, dados algunos atributos de un cliente, puede predecir las probabilidades de que este abandone la relación.
Problemas de Clasificación
Supongamos que se le ha encomendado la tarea de construir un modelo para predecir si un producto comprado por un cliente será devuelto o no. Dado que hasta ahora nos hemos centrado en modelos de regresión, imaginemos si estos serán adecuados en este caso.
Un modelo de regresión generará valores continuos como salida (por ejemplo, 0,1, 100, 100,25, etc.), pero en nuestro caso práctico solo tenemos dos valores como salida: si un producto se devolverá o no se devolverá.
En tal caso, excepto estos dos valores, todos los demás serán incorrectos o no válidos. Si bien podemos decir que el producto devuelto se puede considerar como el valor 0 y el producto no devuelto como el valor 1, aún no podemos definir qué significa un valor de 1,5.
En escenarios como estos, los modelos de clasificación entran en escena. Los problemas de clasificación son el tipo más común de problema de aprendizaje automático.
Las tareas de clasificación se diferencian de las tareas de regresión en que, en las tareas de clasificación, predecimos una etiqueta de clase discreta (por ejemplo, si el producto se devolverá o no), mientras que, en el caso de la regresión, predecimos valores continuos (por ejemplo, el precio de una casa, la edad de una persona, etc.).
Otra diferencia notable entre los problemas de clasificación y los de regresión radica en la elección de las métricas de rendimiento. En los problemas de clasificación, la precisión se suele elegir como métrica de rendimiento, mientras que la raíz cuadrada media es bastante común en el caso de la regresión.
Existen muchos casos de uso empresarial importantes para problemas de clasificación donde la variable dependiente (también denominada variable objetivo, que es el valor que intentamos predecir) es discreta, como la pérdida de clientes o la detección de fraude. En estos casos, la variable de respuesta solo tiene dos valores: pérdida o no pérdida, y fraude o no fraude.
Por ejemplo, supongamos que queremos predecir si un cliente perderá (y = 1) o no (y = 0) tras contratar un servicio móvil. En este caso, la probabilidad de que un cliente pierda se indica como p = P(Churn), y la posible variable explicativa x incluye la antigüedad de la cuenta, el importe de la facturación actual y el promedio de días de mora (es decir, el promedio de días que una persona no realiza su pago). La siguiente figura ilustra cómo funciona una tarea de clasificación supervisada.
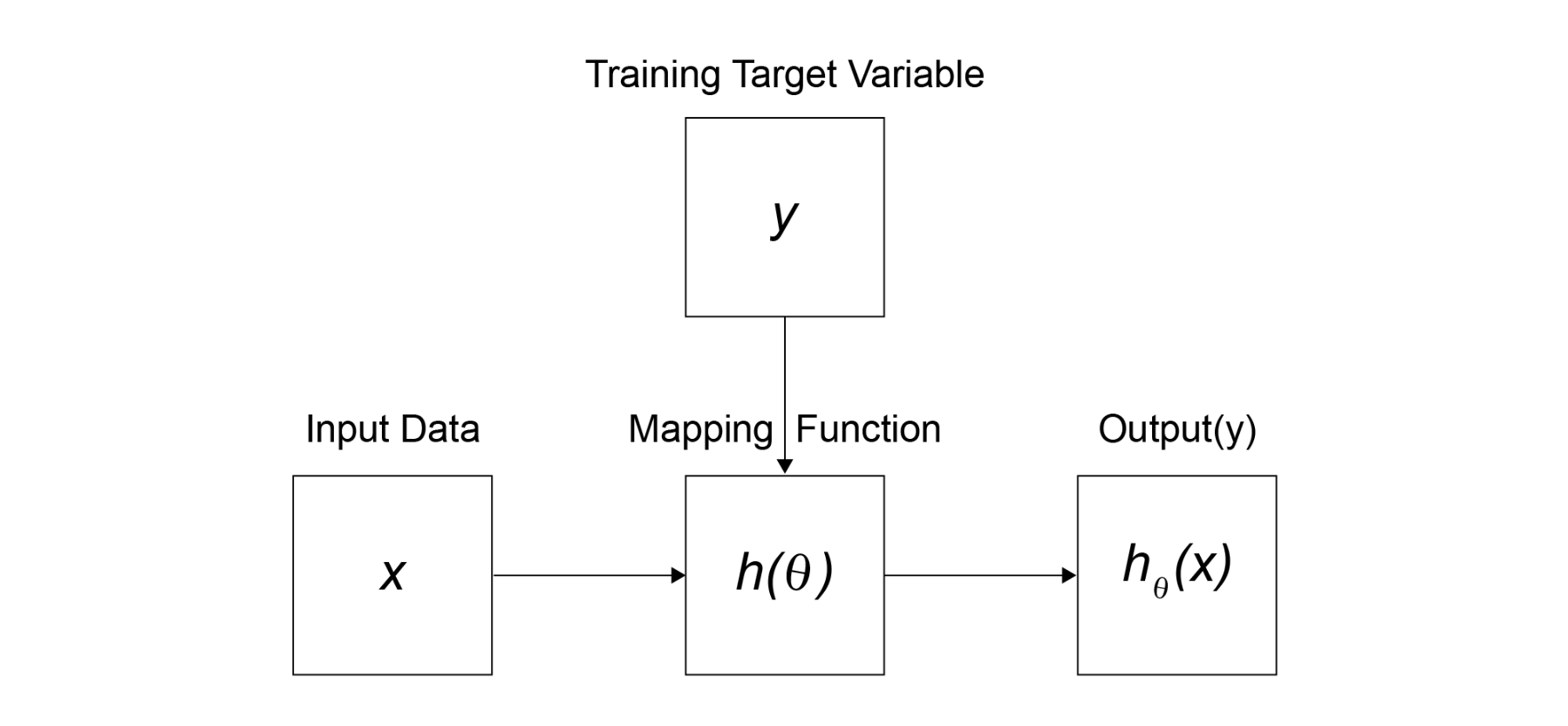Figura 11.10 - Un conjunto de modelos de árboles
Como supervisores, proporcionamos al modelo las variables (x, y), lo que le permite calcular el parámetro theta (θ). Este parámetro se aprende de los datos de entrenamiento y también se denomina coeficiente. x incluye las variables explicativas e y es la etiqueta objetivo que proporcionamos al modelo para que aprenda los parámetros.
Con esto, el modelo genera una función h(θ), que asigna la entrada x a una predicción hI(x). Para el caso práctico de predicción de abandono, x se referirá a los atributos del cliente, que se incorporarán a la función de mapeo h(θ) para predecir la probabilidad de abandono del cliente (variable objetivo y).
Los problemas de clasificación generalmente se dividen en dos tipos:
Clasificación binaria: La variable objetivo solo puede tener dos valores categóricos o clases. Por ejemplo, dada una imagen, se clasifica si es un gato o no.
Clasificación multiclase: La variable objetivo puede tener múltiples clases. Por ejemplo, dada una imagen, se clasifica si es un gato, un perro, un conejo o un pájaro.
Ahora que hemos repasado los fundamentos de una tarea de clasificación supervisada, comencemos a aprender el modelo de referencia comúnmente utilizado en la clasificación: la regresión logística.
¿Qué es la regresión logística?
La regresión logística es un modelo estadístico utilizado para predecir la probabilidad de que ocurra un evento binario, como:
- ¿Cliente comprará? Sí / No
- ¿Email es spam? Sí / No
- ¿Paciente tiene una enfermedad? Sí / No
¿Cómo funciona?
A diferencia de la regresión lineal, la regresión logística modela la probabilidad utilizando la función sigmoide:
p = 1 / (1 + e^-(β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ))El resultado es un valor entre 0 y 1 que representa la probabilidad de que la clase sea "1".
Función sigmoide
La función sigmoide transforma cualquier número real en un valor entre 0 y 1:
Interpretación de los coeficientes
Cada coeficiente (β) indica el efecto de la variable independiente sobre el log-odds (logaritmo de la razón de probabilidades).
Ejemplo: si β₁ = 0.7, un aumento en x₁ incrementa la probabilidad del evento.
Evaluación del modelo
- Accuracy: Porcentaje de predicciones correctas
- Precision / Recall: Métricas clave en clasificación
- Curva ROC y AUC: Evaluación de la capacidad discriminativa
- Matriz de confusión: Resumen de predicciones vs reales
Aplicaciones comunes
- Marketing: Probabilidad de conversión
- Finanzas: Riesgo de incumplimiento
- Salud: Diagnóstico de enfermedades
- Seguridad informática: Detección de intrusiones
Supuestos de la Regresión Logística
A diferencia de la regresión lineal, la regresión logística tiene supuestos particulares:
1. No se asume linealidad
La regresión logística no asume una relación lineal entre las variables independientes (x) y la variable dependiente (y).
2. Variable dependiente binaria
La variable objetivo debe ser binaria, es decir, tener solo dos categorías posibles (por ejemplo, "Sí" o "No").
3. Sin requerimientos sobre variables independientes
- No es necesario que las variables independientes tengan intervalos iguales
- No deben seguir una distribución normal
- No es necesario que tengan varianzas iguales entre grupos
- No se requiere relación lineal con la variable dependiente
4. Categorías excluyentes y exhaustivas
Las categorías de la variable dependiente deben ser mutuamente excluyentes y exhaustivas:
- Cada observación debe pertenecer a una sola categoría
- Las categorías deben cubrir todos los posibles estados